딥러닝이란?(3)

개발 일지/기타

딥러닝이란?(3)

DDD Developer 2024. 10. 25. 14:08

728x90

딥러닝은 뭘 보고 공부하나?

▶ 인간도 마찬가지입니다. 대체 뭘 보고 공부할까요?

▶ 우리는 어떤 공부를 할 때 이해를 기초로 하여 그 원리를 깨닫고 이를 해석할 수 있는 실력을 기릅니다.

▶ 하지만 그렇다고 한 들 '학습이 잘 되었는가?'는 판단하려면 꼭 거쳐야 하는 것이 있습니다.

▶ 바로 '시험'입니다.

▶ 시험 점수만 봐도 학습을 제대로 했는지 덜 했는지 판단할 수 있습니다.

▶ 그리고 딥러닝의 학습에도 이런 '시험' 같은 존재가 존재하고 이를 통해서 딥러닝은 학습을 진행합니다.

▶ 그리고 이미 우리는 그 방식을 사용해서 이미 AND와 OR, XOR을 만들어보았습니다.

▶ 바로 '손실 함수(Loss Function)'입니다.

손실로 평가하다

▶ 인간에 대한 비유를 해봤으니 더 해보겠습니다.

▶ 앞선 손실 함수의 값은 0에 가까울수록 좋다고 했습니다.

▶ 그런데 인간의 시험은 100점이라던가 만점과 같이 점수가 높을수록 좋은 체계를 선택했습니다.

▶ 그런데 Loss Function은 오히려 적을수록 좋은 체계를 선택했습니다.

▶ 이는 우리가 학습한 결과와 실제 정답간의 '오차(Error)'를 줄이는데 집중하기 위해서입니다.

▶ 즉, 오차가 적다는 것은 그만큼 다르지 않다는 의미이고 이것은 곧 잘 맞췄다는 의미일 것입니다.

▶ 더군다나 0으로만 향하면 되는 손실 함수와는 다르게 특정 점수로 향하게 된다면 몇몇 데이터는 점수를 부여하는 것 자체가 난이도가 있는 문제 또한 존재할 것입니다.

▶ 때문에 우리는 이 '오차'가 최소한으로 나오도록 만드는 것에 집중하는 것입니다.

▶ 자, 그럼 0으로 향해야 되는 것은 알았습니다.

▶ 그런데 Loss Function의 문제점은 '데이터마다 측정하는 방식이 다르다'가 문제입니다.

▶ 엄청나게 끔찍한 걸 상상합니다. 어떻게 평가하는가?

▶ 다만, 선형대수학의 방식을 이용한다면 크게 어렵진 않습니다.

▶ 우선 그 계산 방식과 그 계산 방식이 효율적이고 좋은 방식이더라 는 증명 부분은 수학적으로 복잡하고 수식도 귀찮습니다.

▶ 때문에 우리는 '어떠한 데이터를 어떻게 작업할 때 어떤 손실함수가 좋다'라는 측면을 기준으로 Loss Function에 대해서 이해해보겠습니다.

▶ 그럼에 앞서 그럼 어떤 계산을 하길래 오차(Error)를 구해내는지 확인해보겠습니다.

보석상이 100만원 손해

▶ 밈으로나 돌아다니는 그런 이야기이긴 합니다.

▶ 하지만 이 손해라는 것도 해석하자면 '손실'일 것입니다.

▶ 자, 거래를 한다고 생각해보겠습니다. 그런데 살짝 이벤트가 벌어진 것 같습니다.

▶ 특정 가격이 책정된 물건이 있습니다. 우선 1000원인데 고객인 우리는 이를 모른다고 가정하겠습니다.

▶ 그리고 가게 주인이 이 물건의 가격을 역으로 물어봅니다. 우리는 그 가격을 예측해서 말하게 될 것입니다.

▶ 딱 맞게 말할 경우 우리는 공짜로 물건을 가져갈 것입니다. 하지만 크거나 작게 말하면 그만큼 차익을 돈을 내야합니다.

▶ 우리의 목표는 '정확하게 가격을 부르는 것'이 될 것입니다.

▶ 손실이 가장 적인 것이 바로 우리가 원하는 목표인 셈입니다.

▶ 때문에 손실함수를 '목적 함수(Object Function)'라고도 부르기도 합니다.

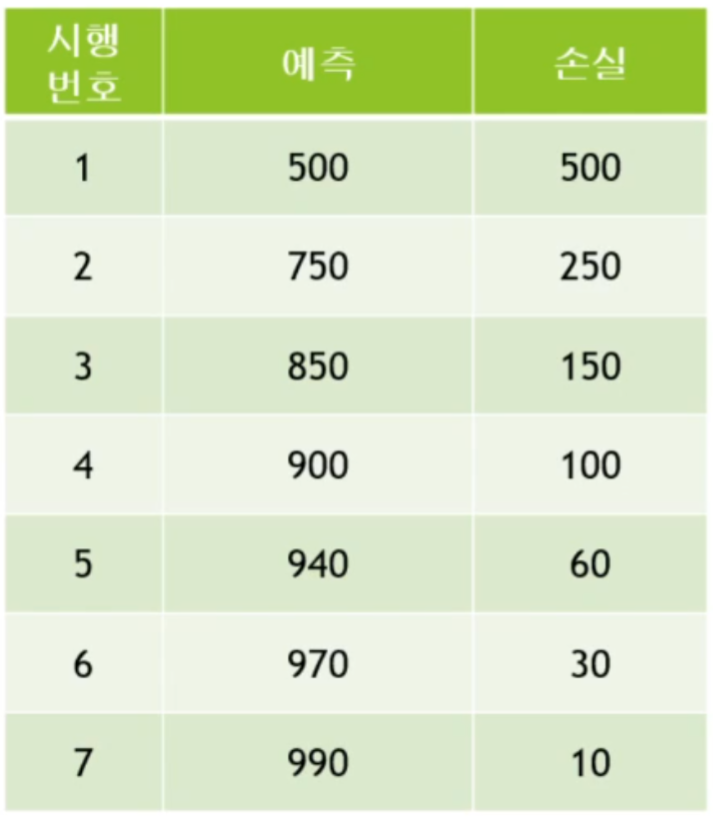
▶ 이제 그냥 고객이 딥러닝 모델이라고 생각해봅시다.

▶ 아마 다음과 같이 작동했을지 모릅니다.

▶ 물론 기본적인 사람이라면 바로 750원에서 250원이 나왔다면 1000원을 불렀을 것입니다.

▶ 뭐 그거야 인간의 기본적인 추론 판단이고 딥러닝은 그런 '패턴'자체를 아직 학습하지 않았으니 이렇게 다가가는 것이 맞는 셈이죠.

▶ 이처럼 우리가 어떤 결과를 얻기 위해 사용한 '비용'이라는 측면에서 '비용 함수(Cost Function)'라는 말도 사용됩니다.

Loss, Cost,Object

▶ 이런 상황에 처하면 다들 그런 말 할 겁니다.

▶ '그럼 언제 저 단어들을 써야하나요?'

▶ 이를 이해하면 어느 순간에 쓰면 되는지 알겠지만 그럴 시간이 없는 입장에서는 명확하게 답 하나 말해주는게 더 빠를 것입니다.

▶ 그냥 항상 평가에 사용되는 함수는 'Loss Function(줄여서 Loss)'라고 생각하면 됩니다.

▶ 다만, Cost Function이나 Object Function이라는 용어를 쓰는 경우가 있더라도 이를 'Loss'라고 해석하여 놓치지 않아야 된다는 말입니다.

▶ 전체적인 흐름에 맞춰서 용어를 달리 쓰긴 하지만 결국 목적은 같은 것이기 때문입니다.

▶ 그리고 결국 최적화 함수가 보고 판단하는 것은 실질적으로 'Loss'이기도 하고요.

작업별 Loss Function

▶ 그럼 어떻게 나뉘어질까요?

▶ 앞선 방식에 따라 달라집니다.

▶ Regression 같은 경우에는 MSE, MAE, RMSE 등이 존재합니다.

▶ 만약, 분류라면, 'Binary Cross Entropy', 'Categorical Cross Entropy', 'Sparse Categorical Cross Entropy'와 같은 것들이 사용됩니다.

▶ Segmentation은 'Catgorical Cross Entorpy', 'IoU', 'Dice'와 같은 것을 사용하고, Object Detection은 위치 점수와 정답 점수를 합친 Total Loss 같은 것을 사용합니다.

▶ 어쨌든, 이 Loss Function을 무엇을 쓰냐에 따라 구조는 같아도 전혀 다른 결과를 초래할 수 있으며 일부 경우 학습이 되지 않는 경우도 발생하는 만큼 구조와 더불어 신경써서 설정해줘야 하는 함수입니다.

MAE(Mean Absolute Error)

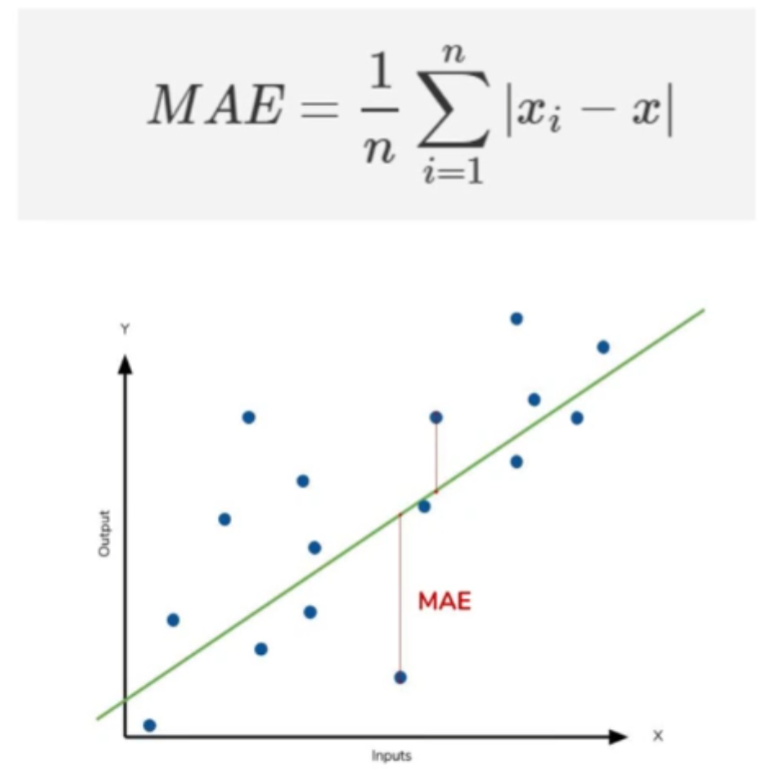
▶ 절대값 평균 에러라고 부르는 이 방식은 Regression에 자주 사용되는 Loss입니다.

▶ 예측값과 실제 값을 비교하고 이 때의 차이의 값을 순수하게 절대값(Absolute)으로만 계산하여 그 차이를 계산하여 모두 합한 값을 값으로 가집니다.

▶ 가장 간편한 수식으로 표현이 가능하지만 단점은 순수 거리로만 계산하기 때문에 (1, 1) 평균이나 (2, 0) 평균이 같아 평균의 함정에 빠지기 쉽다는 것입니다.

▶ 이를 해결할 수 있는 방법이 바로 MSE와 RMSE입니다.

MSE(Mean Squared Error), RMSE(Root MSE)

▶ 제곱 평균 오차, 루트 제곱 평균 오차라고 부릅니다.

▶ 우선 차이를 구하는 것은 MAE와 같으나 이를 절대값이 아닌 제곱을 실시합니다. 이 경우 앞선 (1, 1), (2, 0) 문제가 다음처럼 (1, 1), (4, 0)이 되면서 평균의 함정에서 벗어날 수 있습니다.

▶ 다만, 수치가 너무 크기 때문에 너무 빠르게 동작할 수 있기 때문에 이를 Root값을 씌운 RMSE와 같은 것도 사용합니다.

▶ 단순 MSE에 Root를 씌운 값이기 때문에 RMSE를 제곱하면 MSE가 된다는 사실을 알아두면 편합니다.

직접 Regression Loss 정해보기

▶ 예제를 작성해보겠습니다.

▶ 우선 코드는 MAE로 되어 있으니 MSE에 대해서도 만들어봅시다.

▶ 더불어 학습된 결과를 보고 학습이 잘 되었는지 판단해 보세요.

# 필요한 라이브러리를 임포트합니다.
import matplotlib.pyplot as plt  # 그래프를 그리기 위한 라이브러리
from sklearn.datasets import load_diabetes  # 당뇨병 데이터셋을 불러오기 위한 라이브러리

import keras  # 딥러닝 모델을 만들기 위한 라이브러리
from keras import layers  # 딥러닝 모델의 레이어를 사용하기 위한 라이브러리

# 랜덤 시드를 설정하여 결과를 재현 가능하도록 합니다.
keras.utils.set_random_seed(0)

# 당뇨병 데이터셋을 불러옵니다.
load_data = load_diabetes()

# 데이터셋에서 입력 데이터(x)와 출력 데이터(y)를 분리합니다.
x = load_data.data  # 입력 데이터
y = load_data.target  # 출력 데이터
size = x.shape  # 입력 데이터의 형태를 저장합니다.

# 딥러닝 모델을 생성합니다.
model = keras.Sequential([
    layers.Dense(units=10, input_shape=(size[1], ), activation='relu'),  # 첫 번째 은닉층: 10개의 뉴런, ReLU 활성화 함수 사용
    layers.Dense(units=256, activation='relu'),  # 두 번째 은닉층: 256개의 뉴런, ReLU 활성화 함수 사용
    layers.Dense(units=1),  # 출력층: 1개의 뉴런 (회귀 문제이므로 활성화 함수 사용 안 함)
])

# 모델을 컴파일합니다.
model.compile(optimizer='adam', loss='mse')  # 옵티마이저: Adam, 손실 함수: MSE

# 모델을 학습시킵니다.
history = model.fit(x, y, epochs=100)  # 입력 데이터(x)와 출력 데이터(y)를 사용하여 100 에포크 동안 학습

# 학습 과정에서의 손실 값을 저장합니다.
history_ = history.history

# 손실 값을 그래프로 표시합니다.
plt.plot(history_['loss'])  # 에포크에 따른 손실 값을 그래프로 그림

# 그래프를 화면에 출력합니다.
plt.show()

직접 Regression 평가해보기

▶ 이제 평가를 해보겠습니다.

▶ 학습이 잘 되었느냐? 학습은 loss가 줄어들었다면 학습을 진행을 한 것이니 학습은 되었습니다.

▶ 그러나 학습이 되었다는 것이 '정답을 잘 찾는'이 되는 것이 아닙니다.

▶ 결과를 보았을 때, 실제 값과 100이상 차이나는 경우도 존재합니다.

▶ 이 경우 의료 데이터인 당뇨병 데이터에서 어느정도 신뢰도가 주어져야 한다는 명확한 근거가 있다면 그 수준 안에 들어야 할 것입니다.

▶ 만약 그런 명확한 근거가 없는 비전문적 위치라면 '비교군'을 설정 해야합니다.

▶ 이 모델의 경우에는 기존의 단순 Regression을 한 데이터와 비교해보는 것도 괜찮습니다.

▶ 그보다 좋은 성능이 나왔다면 우리는 '나은 Model'을 얻은 것이 될 겁니다.

Binary Cross Entropy(이진 교차 엔트로피)

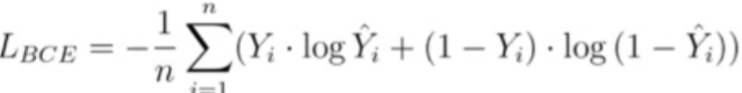
▶ 엔트로피 또한 물리량의 성질을 가져와 활용한 Loss Algorithm입니다.

▶ 뭐 수식도 복잡하고 계산하려면 머리도 아픕니다.

▶ 단순히 가져와 사용하면 되므로 이것이 어떤 곳에 사용되는지만 알면 좋습니다.

▶ 정수 0과 1로 나눠진 이진 분류(Binary Classification) 문제에서 사용되는 Loss입니다.

▶ 분류 문제는 MSE와 같이 계산이 불가능합니다. 왜냐면 0과 1은 그저 분류를 나눠놓은 수이지 이것이 숫자의 의미인 0과 1이 아니기 때문입니다.

Categorical Cross Entropy (다중 클래스 교차 엔트로피)

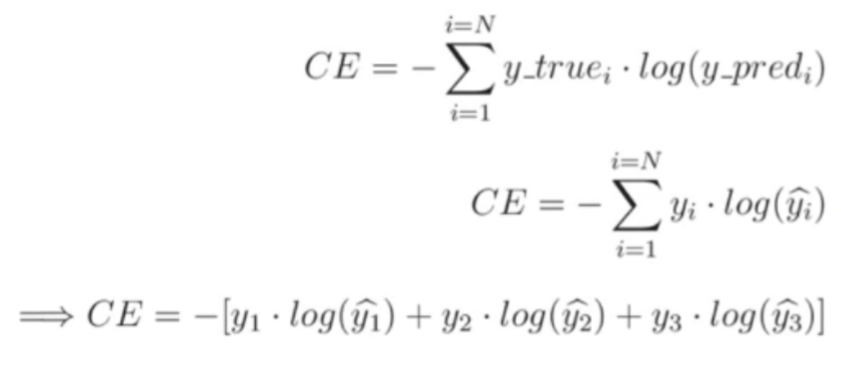
▶ 이번에도 수식은 알바 아닙니다. 중요한 것은 원-핫 인코딩(One-Hot Encoding) 된 다중 클래스 분류(Categorical Classification) 문제에 사용되는 Loss Function이라는 것입니다.

▶ 어쨌든 Class가 3개 이상일 경우 이를 처리하는데 특화되어 있습니다.

*원-핫 인코딩(One-Hot Encoding) 0과 1로만 이루어진 하나의 Vector의 형식으로 Class를 구분하는 형태. 3개를 구분하는 문제에서 1, 2, 3번은 각각 다음과 같이 표현합니다. [1, 0, 0], [0, 1, 0], [0, 0, 1]

Sparse Categorical Cross Entropy(스파스 다중 클래스 교차 엔트로피)

▶ Categorical Cross Entropy와 동일하게 작동합니다.

▶ 다만, One-Hot Encoding을 해야하는 것과 달리 정수형 1개로 처리된 Categorical Classification에 특화되어 있습니다.

▶ 즉, 기존 클래스 분류를 굳이 One-Hot Encoding으로 바꿀 필요 없이 사용하면 됩니다.

▶ 하지만 데이터가 애초에 One-Hot Encoding으로 되어 있다면 굳이 정수형으로 바꾼 뒤 적용하거나 할 필요 없이 상황에 맞게 둘을 나눠서 사용하면 됩니다.

직접 Classification Loss 정해보기

import matplotlib.pyplot as plt  # matplotlib 라이브러리에서 pyplot 모듈을 plt라는 이름으로 가져옵니다.
import numpy as np  # numpy 라이브러리를 np라는 이름으로 가져옵니다.
from sklearn.datasets import load_iris  # scikit-learn 라이브러리에서 iris 데이터셋을 불러옵니다.
from keras import layers  # keras 라이브러리에서 layers 모듈을 가져옵니다.
import keras  # keras 라이브러리를 가져옵니다.

keras.utils.set_random_seed(0)  # 랜덤 시드를 0으로 설정하여 결과를 재현 가능하도록 합니다.

load_data = load_iris()  # iris 데이터셋을 불러옵니다.

x = load_data.data  # iris 데이터셋에서 입력 데이터를 x에 저장합니다.
y = load_data.target  # iris 데이터셋에서 타겟 변수를 y에 저장합니다.
classes = len(np.unique(y))  # 타겟 변수의 고유한 값의 개수를 classes에 저장합니다.
size = x.shape  # 입력 데이터의 형태를 size에 저장합니다.

model = keras.Sequential([  # Sequential 모델을 생성합니다.
    layers.Dense(units=4, input_shape=(size[1],), activation='relu'),  # 4개의 유닛을 가진 Dense 레이어를 추가합니다. 활성화 함수는 ReLU입니다.
    layers.Dense(units=32, activation='relu'),  # 32개의 유닛을 가진 Dense 레이어를 추가합니다. 활성화 함수는 ReLU입니다.
    layers.Dense(units=64, activation='relu'),  # 64개의 유닛을 가진 Dense 레이어를 추가합니다. 활성화 함수는 ReLU입니다.
    layers.Dense(units=classes, activation='softmax'),  # classes 개수의 유닛을 가진 Dense 레이어를 추가합니다. 활성화 함수는 softmax입니다.
])

# 모델을 컴파일합니다. 옵티마이저는 Adam, 손실 함수는 sparse_categorical_crossentropy, 평가 지표는 accuracy입니다.
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy']) 
history = model.fit(x, y, epochs=100)  # 모델을 학습합니다. epochs는 100입니다.

history_ = history.history  # 학습 히스토리를 history_에 저장합니다.

plt.plot(history_['loss'])  # 학습 히스토리에서 loss 값을 그래프로 그립니다.
plt.show()  # 그래프를 표시합니다.

plt.plot(history_['accuracy'])  # 학습 히스토리에서 accuracy 값을 그래프로 그립니다.
plt.show()  # 그래프를 표시합니다.

▶ 예제를 작성해보겠습니다.

▶ 단, 이전과 다르게 Binary Cross Entropy가 아니라면 최종적으로 출력층의 units는 분류하고자 하는 클래스의 개수를 넣습니다.Categorical은 활성화 함수로 Softmax, Binary의 경우 Sigmoid를 활성화 함수로 사용합니다.

▶ 이전 연속적인 수가 아닌 Classification을 위한 값은 정확도(Accuracy) 측정이 가능합니다. 이에 compile시 accuracy를 지표로 출력해주도록 할 수 있습니다.

직접 분류 평가해보기

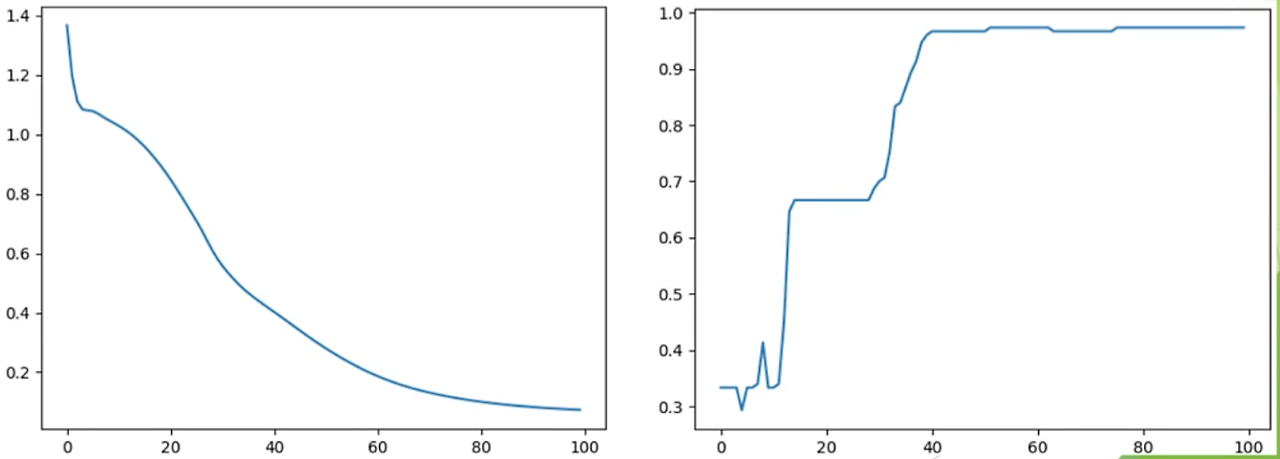
▶ 두 그래프는 각각, Epoch별 Loss와 Epoch별 정확도입니다.

▶ 학습도 잘했으며, 이전 분류 기록을 본다면 90대의 정확도면 꽤나 정확합니다.

▶ 이는 꽤나 잘 결과를 낸 셈입니다.

분류 성능 평가 지표

▶ 물론 이렇게 정확도를 측정하는 것으로 분류 성능을 측정할 수는 있으나 다른 방식으로도 가능합니다. 그리고 이 방식은 이후 설명할 Object Detection에서 흔한 방식에서도 사용됩니다.

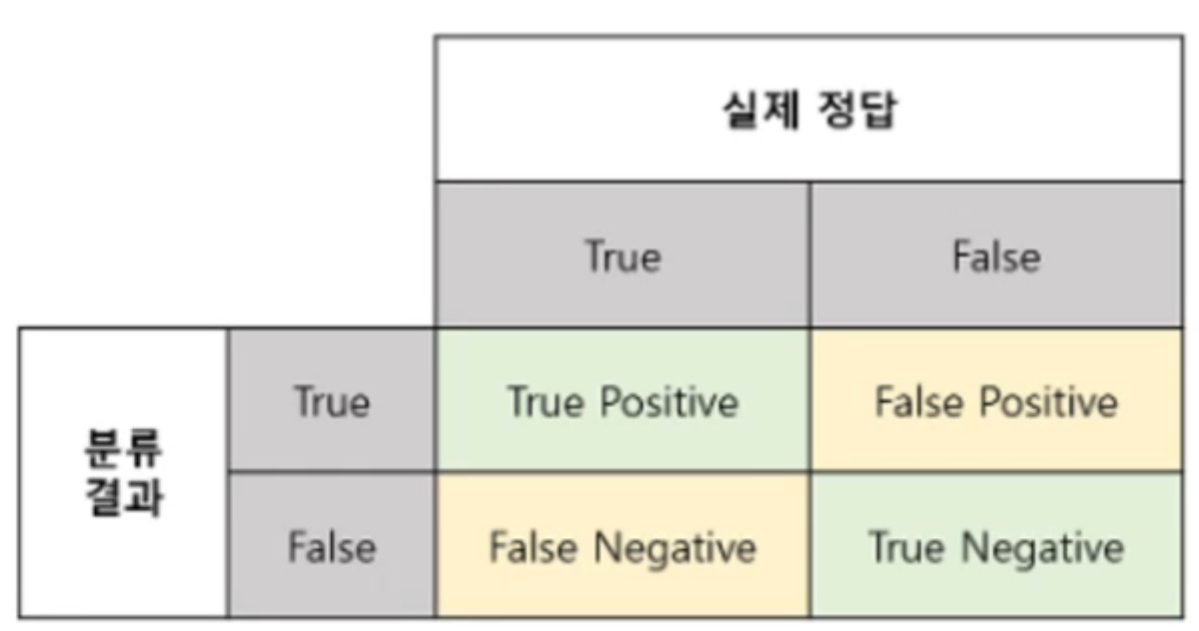
▶ 분류성능평가지표는 다음과 같은 분류를 우선 알아야합니다.

▶ 경우의 수는 총 4가지 입니다. 정답인데 정답이라고 한 경우(TP), 정답인데 정답이 아니라고 한 경우(FN), 정답이 아닌데 정답이라고 한 경우(FP), 정답이 아닌데 정답이 아니라고 한 경우(FN).

▶ 이 경우 두가지 수치로 이를 해석할 수 있습니다.

▶ 하나는 정밀도(Precision)이고 하나는 재현율(Recall)입니다.

▶ Precision은 Model이 정답이라고 찾은 것들 중에 실제 정답인 경우, 즉 정확도에 대한 데이터이고, Recall은 실제 정답이라고 찾은 것들 중에서 모델이 정답이라고 한 경우, 즉, 실현 정도에 대한 수치입니다.

▶ 자세한 건 따로 다루겠습니다.

IoU(Intersection over Union)

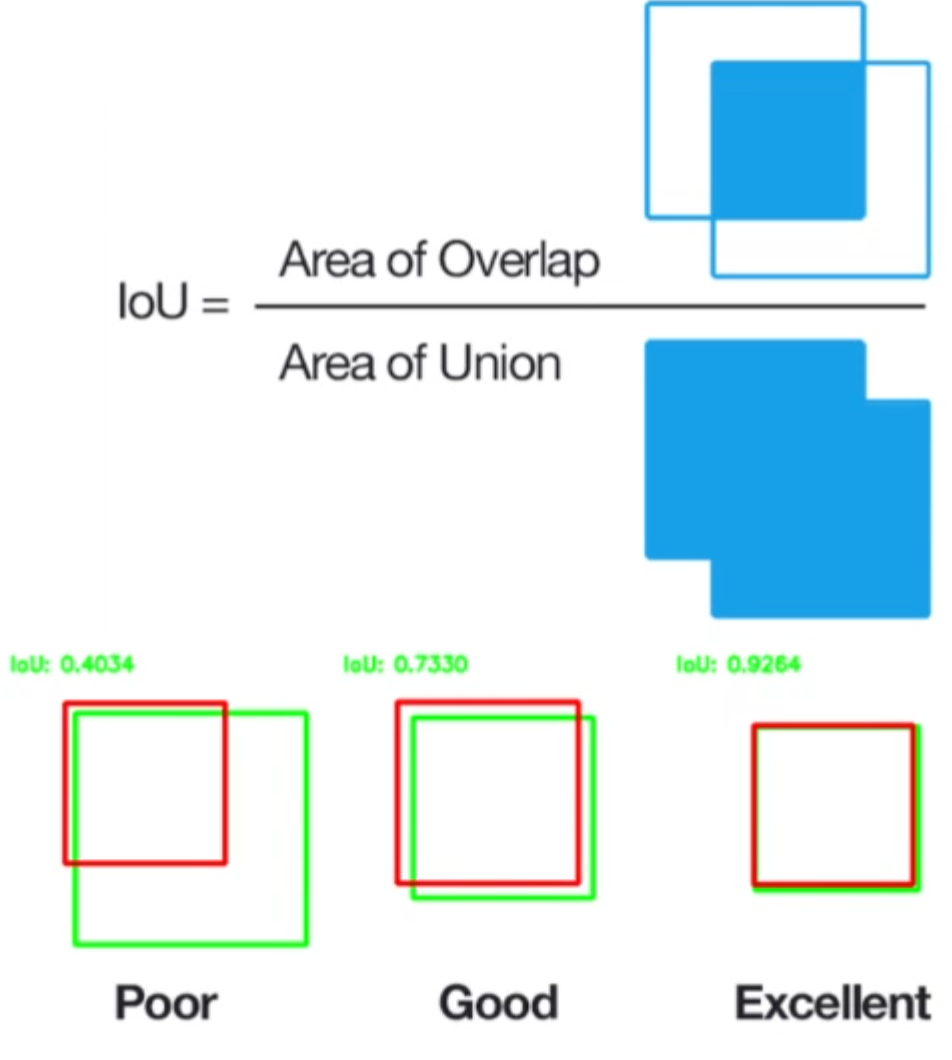
▶ IoU는 Segmentation이나 Object Detection에 사용되어지는 손실 함수입니다.

▶ 이미지에서 특정 구역의 위치 특정에 대한 Score입니다.

▶ 예를 들면 교실 사진에서 사람들의 수를 세려면 사람들만 특정해야 하는데 이때, 특정한 위치가 실제 사람으로 표시한 부분과 일치함에 대한 점수입니다.

▶ 위치에 대한 점수이기 때문에 일전 분류성능평가지표도 같이 제공되어야 합니다.

▶ 분명 똑같은 위치를 짚었지만 다른 분류를 할 수도 있으면 정확한 것이 아니기 때문입니다.

Total Loss

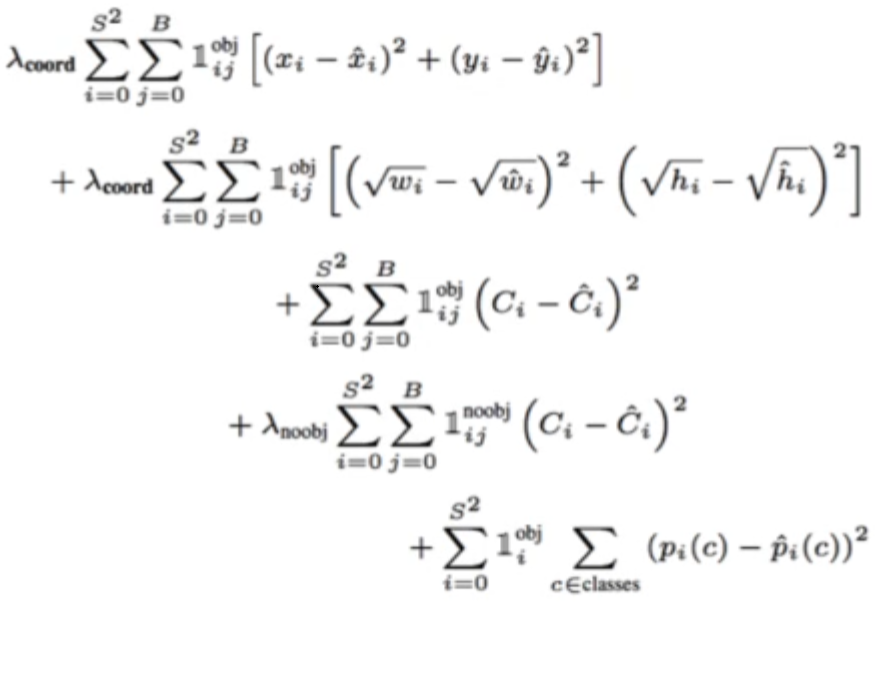
▶ 하지만 결국 이를 역전파하고 최적화 함수가 최적의 수치로 변화를 하려면 결국 1개의 Loss로 평가를 해야 합니다.

▶ 때문에 위치를 잘 특정한 손실 함수의 클래스를 잘 분류한 손실 함수의 값을 적절히 조합해야 합니다.

▶ 그리고 이 손실 함수는 그에 대한 부분입니다.

▶수식도 어렵고 증명도 어려운 편입니다.

▶ 다행인 것은 우리가 그저 가져가서 활용을 하면 된다는 점일 것입니다.

그 외의 손실 함수

▶ 물론 여전히 수 많은 손실 함수들이 등장하고 사라지고 있습니다.

▶ 시간도 성능도 모두 만족하는 손실 함수가 있으면 좋겠지만 아직 그렇지 않다는 한계가 있습니다.

▶ 아마 대중적인 문제 풀이에는 대중적인 손실 함수를 쓸테지만 언젠가 대중적인 문제 풀이가 아닌 문제를 풀게 된다면 그 숨겨진 손실 함수를 찾게 될 것입니다.

딥러닝

▶ 이제 겨우 인공신경망의 일반적인 흐름에 대해서 이해하게 되었고 사용할 수 있게 되었습니다.

▶ 하지만 이것이 딥러닝의 끝은 아닙니다.

▶ 아직 우리가 알아야할 개념이 남아있습니다.

▶ 딥러닝은 그 전체적인 형태에 따라 CNN, RNN, GAN 등으로 나뉩니다.

▶ 이제 우리는 CNN, RNN, GAN이 무엇이고 이것이 할 수 있는 일은 무엇이며 이것으로 우리가 무엇을 만들 것인지를 선택해야 합니다.

▶ 그리고 그 이전에 딥러닝에서 활용할 수 있는 것들에 대해서 조금 팁을 주려합니다.

정규화(Normalization)

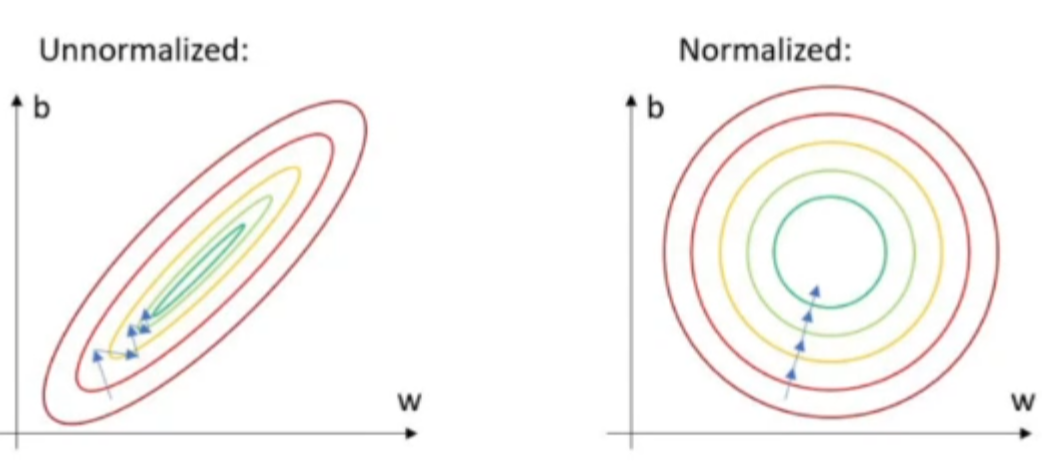
▶ 데이터 중 일부의 경우 그 수치의 차이가 심할 경우가 있습니다.

▶ 단순 단위 문제부터 실제 측정 위치가 다르다던가 하는 문제들이 실존합니다.

▶ 그래프로 그리자면 좌측 이미지처럼 축의 크기가 달라 문제가 생깁니다.

▶ 그렇기 때문에 이를 보정해주어야 합니다.

▶ 머신러닝에서 배웠던 정규화 기법을 그대로 적용하면 됩니다.

▶ 딥러닝을 기준으로 한다면 꼭 정규화해야 하는 이유를 들자면, 연산 속도가 빨라지고, 과적합을 조금 방지할 수 있다는 점을 들 수 있습니다.

정규화(Normalization) 해보기

load_data = load_diabetes()

x = load_data.data
y = load_data.target

norm = layers.Normalization()

norm.adapt(y)

denorm = layers.Normalization(invert=True)

denorm.adapt(y)

y_ = norm(y)

size = x.shape

▶ 정규화 되지 않은 데이터를 정규화 하여 정규화 된 형태로 학습을 한다면 분명 모델이 뱉은 값도 정규화 되어 있는 상태일 것입니다.

▶ 이것은 우리가 원하는 실제 값이 아니니 이것을 다시 역으로 본래의 값으로 되돌려주는 과정도 필요하기 때문에 이를 같이 진행해 줍니다.

▶ 일전 당뇨병 Regression 코드를 활용해보겠습니다. 이 후 학습을 하고 결과를 확인해 보겠습니다.

▶ 정규화 되지 않은 데이터를 정규화 하여 정규화된 형태로 학습을 한다면 분명 모델이 뱉은 값도 정규화되어 있는 상태일 것입니다.

▶ 이것은 우리가 원하는 실제 값이 아니니 이것을 다시 역으로 정규화해주는 과정도 필요하기 때문에 이를 같이 진행해 줍니다.

▶ 일전 당뇨병 Regression 코드를 활용해보겠습니다. 이 후 학습을 하고 결과를 확인해 보겠습니다.

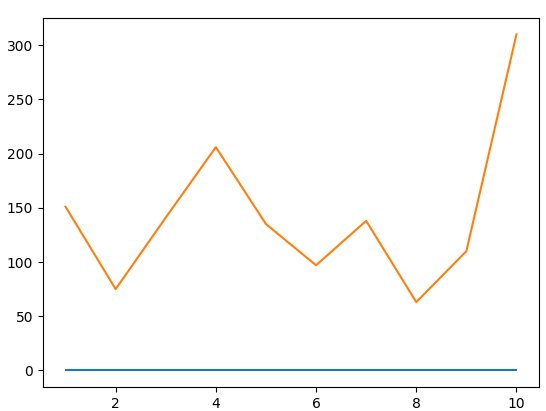
▶ 그래프가 1개가 되었습니다?

▶ 1개가 된 것이 아닙니다. 완벽하게 일치하는 모델이 만들어 진 것입니다.

Epoch와 Batch(배치)

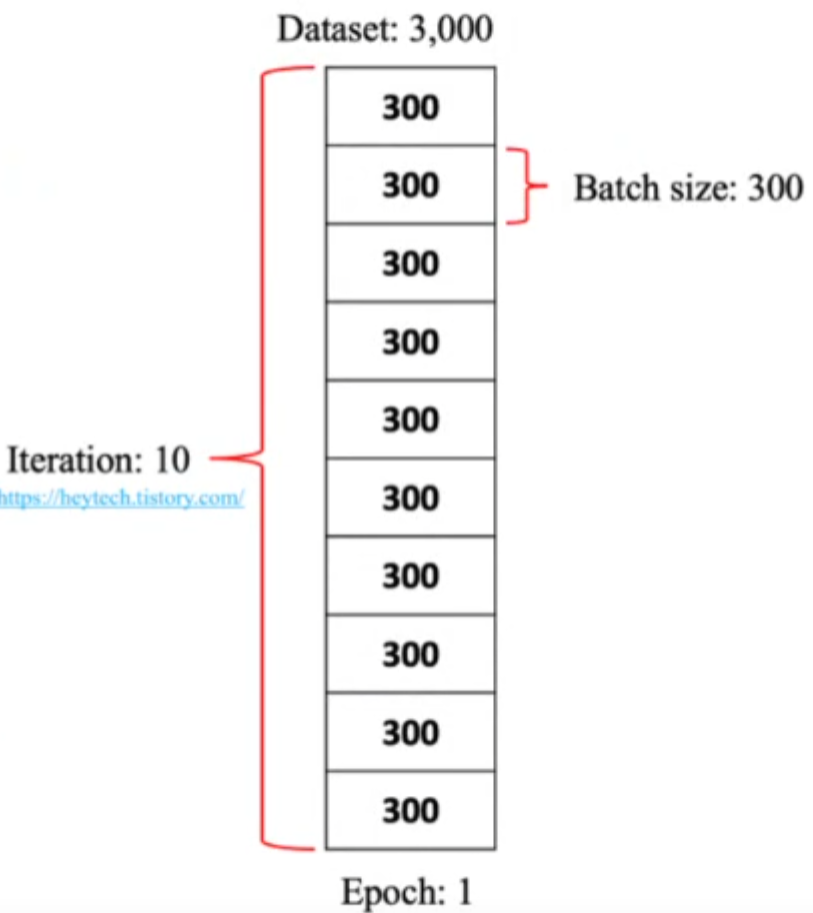
▶ 우리가 학습하고자 하는 데이터는 아마도 엄청 클 것입니다. 그것이 딥러닝의 성능을 위해서도 필요한 요소입니다.

▶ 하지만 '공짜 점심은 없음 정리'에 의해서 결국엔 너무나도 많은 시간이 걸릴 것입니다.

▶ 시간만 문제일까요? 이 모든 데이터를 한꺼번에 메모리에 할당하려고 한다면 컴퓨터는 매우 힘들어 할 것입니다.

▶ 단순 100MB를 불러오고자 하더라도 이를 위한 가중치 데이터와 여러 파라미터들까지 메모리에 존재해야 하니 생각보다 더 큰 메모리가 필요로 할 것입니다.

▶ 그러면 우린 무조건 큰 메모리가 설치된 곳에서만 학습이 가능할까요?

▶ 배치는 데이터마다 크기(Batch size)가 다릅니다. 좌측과 같이 3000을 10등분하겠다는 의미를 가진다면 Batch size는 300이 될 것입니다.

▶ 기준도 다릅니다. Dataset을 N등분하여 Batch size를 정하는 경우도 있고, Batch size를 정해놓고 Dataset이 N등분 되도록 하는 방법이 있습니다.

▶ 의도적이라면 전자도 괜찮지만 우리가 신경써야 하는 것은 '메모리'이니 후자가 훨씬 도움이 될 것입니다.

▶ 다만 배치 사이즈는 전체 Dataset에 비해 너무 작거나 크면 그 의미가 퇴색되기 때문에 적당한 크기에 대한 고민을 해야합니다.

▶ 다만, 아직 경험적인 부분이 없다면 이 '적당히'라는 단어가 어려울 것입니다.

▶ 어머님의 요리처럼 '소금 적당히'라는 말은 경험해보지 않으면 모르는 단위입니다.

▶ 다만, 고려할 점은 다음과 같이 존재합니다.

1.메모리에 충분한 크기인가?

2.데이터가 충분히 고르게 분리되는가? (33개를 10개로 나누면 3개가 남는 배치가 생기는 것과 같은 문제)

3.2의 제곱수인가? (2, 4, 8, 16, 32, 64, 128, 256, 512, ...)

▶ 위 기준에 얼추 취합한다면 크게 신경쓸 요소는 아니라는 점만 인지하시면 됩니다

Epoch와 Batch(배치) 해보기

▶ Iris Classification 코드를 가져와 배치를 사용해보겠습니다.

history = model.fit(x, y, epochs=100, batch_size=16, shuffle=True)

▶ Iris 데이터를 보면 0~2로 3등분이 되어 있기 때문에 배치 단위로 자르게 되면 특정 배치에는 0만, 2만, 3만 존재할 문제가 있습니다. 때문에 이를 방지하기 위해서 섞어주는 행동을 해 주어야 합니다.

▶ 더불어 이 방식은 우선 메모리에 다 할당한 상태에서 배치 사이즈를 나눈 것이므로 메모리적으로는 이점이 없다는 것을 인지해야합니다. 실제 데이터셋 설정시에는 다른 방식을 사용해야합니다. 이는 차후에 데이터가 많아지면 진행해보겠습니다.

▶ 이전보다는 좋은 결과가 나온 것 같습니다. 그리고 보시는 바와 같이 총 한 Epoch에 10번을 반복하는 것을 확인할 수 있습니다. 솔직히 성능적인 향상은 비교하기 어렵고 배치를 만들어 돌렸다는 것에 의의를 두시면 좋겠습니다.

데이터 증강 (Data Augmentation)

▶ 데이터가 너무 부족할지 모릅니다. 그렇다고 있는 것만 돌리기에는 너무 일반화 되어 있지 않을지도 모릅니다.

▶ 이럴 때를 위해서 Data Augmentation이 존재합니다.

▶ 데이터 증강이라는 의미의 이 방식은 우리가 값에 작은 노이즈나 형태 변환을 가한다고 해서 실질적인 정보가 손상되지 않는다는 인식에 기반합니다.

▶ 이미지를 예를 들어 보면 좌측 이미지와 같이 기울이거나, 늘리거나, 이동시키거나 색상을 조금 바꾼다고 해서 우리가 그 이미지에서 '쿼카'를 찾을 수 있다는 것과 같습니다.

▶ 그런데 이런 생각도 할 것입니다.

▶ '단순 노이즈나 형태 변환이 부족한 데이터를 채울 수 있을까?'

▶ 아마 이미지를 다뤄보셨다면 그런 말을 하진 않을 것입니다.

▶ 우리야 객체 단위의 이미지 인식이 쉬우니 별 생각 없지만 선형대수학이 적용된 이미지 입장에서는 단순히 같은 위치의 숫자가 1개 달라져도 완전 다른 이미지로 인식할 수 밖에 없습니다.

▶ 그러나 딥러닝의 방식이라면 그 안에서 동일한 패턴을 찾아내려고 할테니 오히려 데이터 증강을 통해서 공통된 패턴을 찾는 성능 향상을 가져올 수도 있는 것입니다.

데이터 증강 해보기

▶ 아직 이미지를 다루진 않으니 기존의 Iris Classification을 이용해보겠습니다.

load_data = load_iris()

x = load_data.data

y = load_data.target

noise = np.random.normal(loc=0, scale=0.1, x.shape)

noisy_x = x + noise

x_ = np.concatenate(arrays=(noisy_x, x), axis=0)

y_ = np.concatenate((y, y))

classes = len(np.unique(y_))

size = x_.shape

history = model.fit(x_, y_, epochs=100, batch_size=32, shuffle=True)

▶ 다음과 같이 수정한 다음 진행해보겠습니다.

딥러닝 구조 심화

드롭아웃(Dropout)

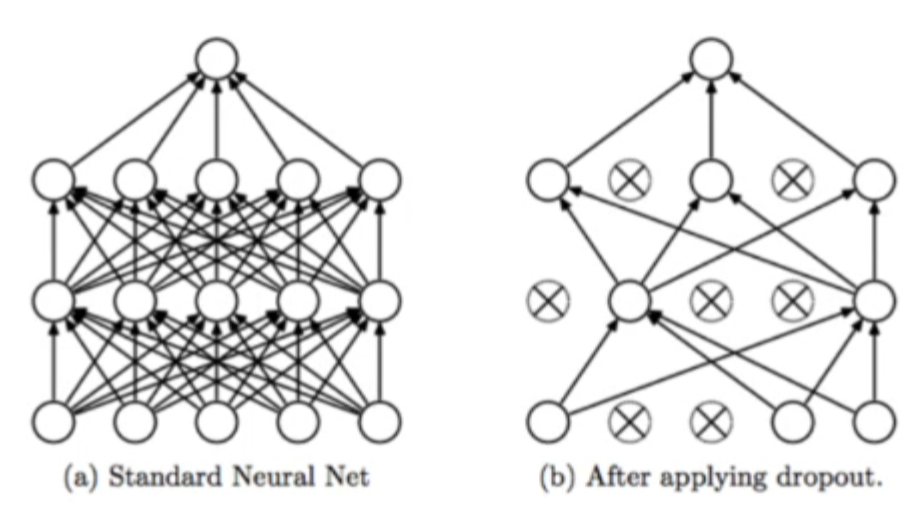
▶ 수많은 정칙화(과적합을 막는 행동) 기법 중 가장 멋지고 쉬운, 그러면서 강력한 기법을 들라고 하면 본인은 '드롭아웃'이라고 할 것이다.

▶ 왜냐하면 드롭아웃 기법은 과적합이 되지 않도록 강력하게 막으면서도 연산도 줄여줄 수 있는 강력한 수단이기 때문입니다.

▶ 게다가 구현도 쉬워 매층마다 추가해주는 것까지 가능합니다.

▶ 원리는 간단합니다. 모든 층은 다음 층으로 각 Node값을 모든 Node으로 전달을 합니다. 하지만 드롭아웃을 적용하게 되면 적용된 층의 설정된 비율만큼의 Node를 해당 학습동안 잠궈버립니다.

model = keras.Sequential([
    layers.Dense(units=4, input_shape=(size[1], ), activation='relu'),
    layers.Dense(units=32, activation='relu'),
    layers.Dense(units=64, activation='relu'),
    layers.Dropout(0.2),
    layers.Dense(units=classes, activation='softmax'),
])

▶ 일전에 사용한 분류 모델입니다. 이곳에 Dropout층 하나를 추가했습니다. 이렇게 추가하게 되면 마지막 은닉층에서 출력층으로 넘어갈 때, 약 20%가 확률적으로 제외되게 됩니다.

▶ 수치로 계산하자면 64 x 0.2 = 7개가 누락되는 것입니다.

▶ 물론 학습해야할 일부를 빼버리는 것이니 전체적인 속도가 느려지는 것은 사실입니다. 하지만 정칙화에서 중요한 것은 과적합을 막는 것입니다.

▶ 어느 층에서든 사용하는 것이 좋으나 대게 은닉층에 적용되도록 하는 것이 좋습니다

history = model.fit(x_, y_, epochs=120, batch_size=32, shuffle=True)

▶ 다만, Dropout 기법 자체가 학습을 몇 개 빼먹어버리는 방식이기 때문에 이를 살짝 보정하기 위해서 20% Epoch를 늘렸습니다.

▶ Dropout이 없이 진행한 모델은 150Epoch로 돌려봐면 더 이상 학습이 되지 않는 구간에 봉착한다는 것을 알게 될 것입니다.

▶ 그에 비해 Dropout은 그 이상으로 학습이 진행되었으며 Loss를 0.05단위까지 성능을 끌어올렸음을 알 수 있습니다.

▶ 이러한 기능 덕택에 Dropout은 가장 간단하면서도 강력한 정칙화 방식이 되었습니다.

배치 정규화 Batch Normalization

▶ 배치 정규화입니다. 일전 데이터에 대해서 다룸에 있어서 정규화에 대해서 이야기했습니다. 이것은 매 배치마다 정규화를 다시 해주는 방식입니다.

▶ 계산식은 좌측과 같습니다만, 딱히 이에 대해서 이해할 필요 없습니다.

▶ 수많은 방식으로 증명하여 이 기능이 정말 학습에 도움이 된다는 것을 이야기할 뿐이니 이 배치 정규화가 하는 일과 능력에 대해서만 이해하면 됩니다.

▶ 이것을 하는 큰 이유는 학습의 효율성과 '기울기 소실' 문제를 해결할 수 있기 때문입니다.

▶ 따로 연산 없이 단순히 층 내부에서 정규화를 해줌으로서 사라져가는 값을 다시금 정규화 된 범위의 값으로 만들어주는 것입니다.

▶ 이렇게 되면 기울기를 계산할 값들이 너무 작지 않게 되고 적당한 기울기 값을 유지할 수 있게 되는 것입니다.

▶ 층이 깊을수록 이 배치 정규화 층이 유의미하게 사용되는 것입니다.

▶ 더군다나 그렇게 많은 연산량을 필요로 하지 않아 효율적입니다.

▶ 마치 필터를 적용한 듯 값이 뻥튀기 되어 다음 층으로 전달해주는 역활을 합니다.

▶ 다만 이를 적용할만큼 큰 딥러닝을 안했기 때문에 예제는 넘어가겠다.

기울기 소실 (Vanishing Gradient)

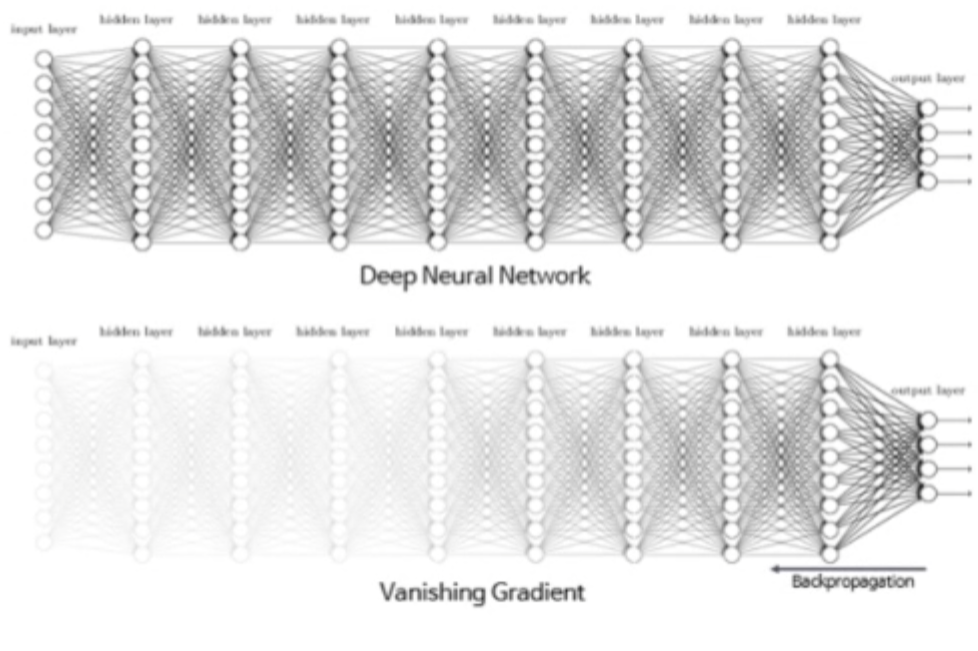
▶ 일전 Sigmoid를 보았던 적이 있을 겁니다. 과거에 인공신경망의 일반적인 활성화 함수는 Sigmoid였습니다.

▶ 하지만 점점 층이 늘어나기 시작하자 Sigmoid는 문제가 발생합니다. 바로 기울기 소실 문제입니다.

▶ 이 기울기 값은 분명 학습을 하는데 중요한 역활을 합니다. 하지만 깊은 층을 이동하다보면 점차 이 기울기가 옅어지기 시작한다는 문제가 있었습니다.

▶ 이것은 Sigmoid 함수의 구조적 문제이기 때문에 당연한 것이었고, 더불어 아무리 이 문제를 어느정도 해결해준 ReLU에서도 발생하는 문제였습니다.

▶ 기울기를 학습의 속도에 가장 큰 방향성으로 잡는 기존의 Optimizer들의 기준에서는 기울기 소실 문제는 학습속도보다는 학습 자체가 멈춰버리는 현상의 문제였습니다.

▶ 생각해보면 모든 수치가 1을 넘기지 않는 활성화 함수 기준에서는 층을 지날수록 원본 아니면 무조건 작아질 수 밖에 없는 운명을 가지고 있었습니다.

▶ 때문에 이를 해결할 여러 방식들이 등장하긴 했습니다.

▶ 그리고 그런 방식들 중 하나로 등장한 것이 바로 'Batch Normalization'입니다.

Validation Data

▶ Validation Data에 대한 설명은 앞서 했으므로 바로 적용을 해보겠습니다.

▶ Tensorflow에서는 미리 데이터셋 단계에서 Validation Data를 분리하거나 학습 중에 구분하도록 하는 방법이 있는데 후자가 우선 쉽게 적용할 수 있으니 해보겠습니다.

history = model.fit(x, y, epochs=120, batch_size=32, 
                    validation_split=.2, validation_batch_size=32,
                    shuffle=True)

▶ 전체 Train Data의 20%를 사용하여 Validation으로 치환합니다. 더불어 Validation Data를 평가함에도 batch로 나누어 검증하도록 합니다.

▶ 이렇게 할 경우 Validation Loss와 Validation Accuracy도 정보로 나오므로 이를 활용하여 그래프를 그려주면 학습에 대해 더 잘 이해할 수 있다.

history_ = history.history

x_range = np.arange(1, len(history_['loss'])+1)

plt.plot(x_range, history_['loss'], x_range, history_['val_loss'])

plt.show()

plt.plot(x_range, history_['accuracy'], x_range, history_['val_accuracy'])

plt.show()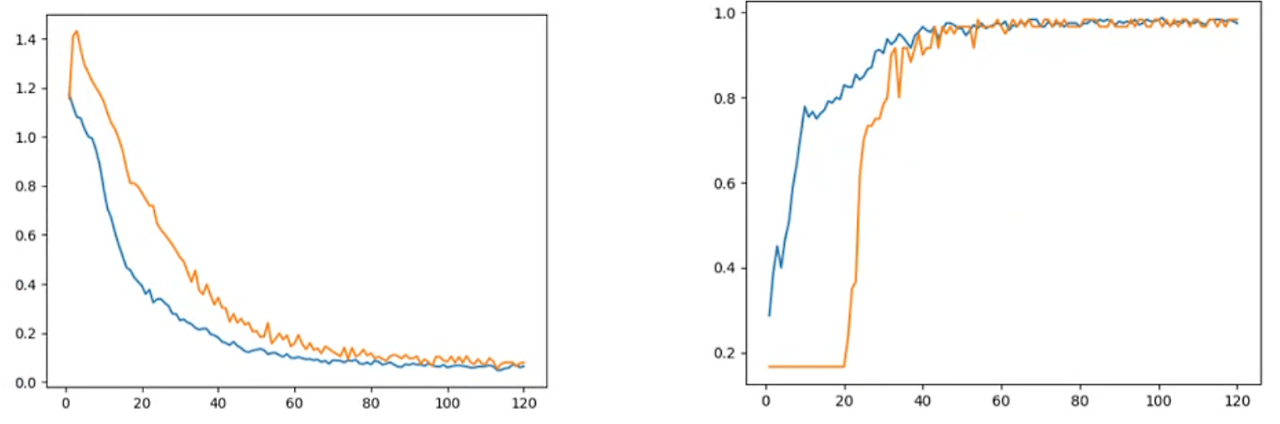

▶ 각각, Loss Graph, Accuracy 그래프에 해당합니다.

▶ 일전에 말했듯이 Train Loss는 Validation Loss보다 아래 있습니다.

▶ 마치 뒤따라가듯한 형태가 일반화가 잘 되어가고 있다는 의미가 됩니다.

▶ 최종적으로는 거의 비슷한 경지에 도달하는데 이는 생각보다 Train과 Validation의 데이터가 유사한 형태를 지녔다는 의미이긴 합니다. 이를 분석을 해야하지만 좋은 결과라고 생각하는 것이 좋겠습니다.

▶ Validation Data는 학습 중 과적합이나 학습 자체에 대한 중요한 지표로 사용이 가능하기 때문에 학습 간에 꼭 지정해주는 것이 효율적입니다.

▶ 물론 그만큼 시간은 소비하게 되고 데이터도 일부 떼어주어야 하는 문제가 있긴 하지만, Validation이 가져다주는 평가적인 의미를 생각해본다면 소소한 문제입니다.

▶ 더불어 이후 설명해줄 'Early Stopping'이나, 'Checkpoint'와 같은 콜백(Callback) 함수를 사용하기에 용이하기 때문에 꼭 설정해주어야 합니다.

▶ 다만, 이 또한 메모리를 잡아먹기 때문에 차후 데이터가 커진다면 단순히 앞선 방식과 같이 fit의 설정으로 지정하는 것이 아닌 Dataset 설정 단계에서 이를 조정해야 합니다.

교차 검정(k-fold Cross-validation)

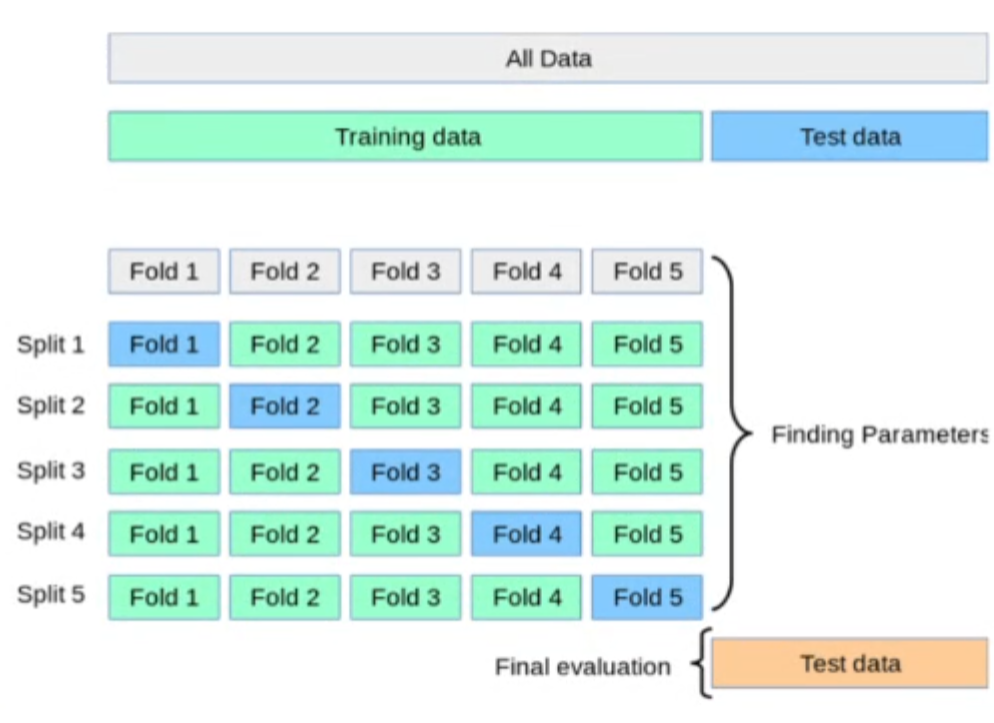
▶ 하지만 데이터가 너무 부족한 상황이라면 어떨까요?

▶ 난이도에 따라 다르겠지만 특정 이상의 비율의 데이터양이 없다면 학습이 잘 되지 않을 것입니다.

▶ 그런데 또 검증은 해야할 때가 있습니다.

▶ 이런 경우에 교차 검정을 사용하면 해결 가능합니다.

▶ 좌측의 이미지와 같이 전체를 학습에 활용할 수도 있지만 더불어 Validation Data의 기능도 사용할 수 있습니다.

▶ 물론 이게 무조건 좋은 것은 아니지만 부득이하다면 이 방식도 괜찮습니다.

Early Stopping(조기 종료)

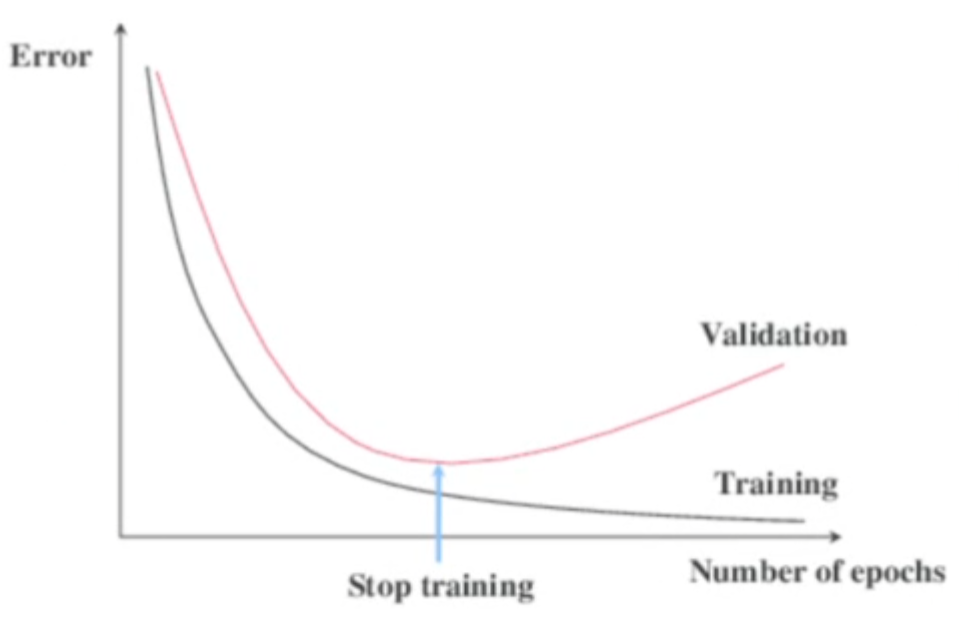
▶ 일반화가 잘 된 모델이 필요한 상황이라면 더더욱 Validation Loss가 정체하거나 상승한다면 학습의 의미가 존재하지 않게 됩니다.

▶ 단순히 시간만 늘어날 뿐입니다.

▶ 하지만 실제 돌려보기 전에는 예측할 수 없는 단위가 될 것입니다.

▶ 하지만 대부분의 그래프 패턴은 좌측과 같이 나타납니다. 한번 양보하더라도 Validation이 정체하는 그래프까지가 가장 일반적인 형태입니다.

▶ 이런 상황에서 굳이 더 학습을 진행할 필요가 없는데 이럴 때 콜백 함수인 Early Stopping을 사용합니다.

Model Checkpoint(모델 체크포인트)

▶ 결국 우리는 어떠한 학습이 완료된 모델을 뽑고 싶은 것이 사실입니다.

▶ 그러나 학습이 끝난 시점의 Model은 과적합이 일어난 시점일 수도 있습니다. 물론 Early Stopping을 이용하면 과적합 이전에 끝낼 수 있지만 이 순간이 최고 성능의 순간은 아니라는 점입니다.

▶ Model Checkpoint는 학습 중 최고 성능의 지점이 발생하면 저장을 하도록 지정하는 콜백 함수입니다.

▶ 이를 통해 과적합 이전에 가장 적절한 Model을 사용할 수도 있으며, 이전 모델들 비교도 해볼 수 있습니다.

콜백(Callback) 함수

▶ 그럼 콜백함수는 무엇일까요?

▶ 재호출 뜻을 가진 콜백 함수는 이벤트 기반 프로그램이나 비동기 프로그램에서 사용되는 함수입니다.

▶ Qt와 마찬가지로 특정 작동이 정의된 프로그램에 커스텀 기능을 넣으려면 이 작동에 방해가 되는 행동은 삼가야합니다.

▶ 때문에 '이벤트 처리'라는 방식을 통해서 동작을 정리하거나, 비동기 프로그램과 같이 언제 어느 순간에 동작이 완료될지 모르는 작업 등을 통제하기 위해서 넣은 함수를 가리킵니다.

▶ 단순히 '어떤 사건이 일어나면 실행되는 함수'의 의미를 가집니다. Qt를 기준으로 둔다면 '클릭을 하면'이라는 신호가 가면 클릭에 대한 콜백 함수가 작동하게 되는 것과 같습니다.

Early Stopping과 Checkpoint

▶ 딥러닝에서는 학습 중에 특정 이벤트 발생시 발동하는 함수를 콜백함수입니다.

▶ 코드는 페이지와 다음과 같습니다.

import matplotlib.pyplot as plt
import numpy as np
from numpy.matrixlib.defmatrix import matrix
from sklearn.datasets import load_iris
import keras
from keras import layers , callbacks
from tensorflow.python.ops.gen_batch_ops import batch

keras.utils.set_random_seed(0)

load_data = load_iris()
x = load_data.data
y = load_data.target
# classes = len(np.unique(y));
# size = x.shape
# 데이터 증강
noise = np.random.normal(0,0.1,x.shape)
noisy_x = x+noise;
x_ = np.concatenate((noisy_x,x), axis = 0)
y_ = np.concatenate((y,y))
classes = len(np.unique(y_))
size = x_.shape

##################################################################
model = keras.Sequential([
    layers.Dense(units=4, input_shape=(size[1],), activation='relu'),
    layers.Dense(units=32, activation='relu'),
    layers.Dense(units=64, activation='relu'),
    # 드롭아웃 : 학습을 생략해버려 속도가 느려집니다. 단 일반화가 훨씬더 잘된다.
    layers.Dropout(0.2), # ㅇ이렇게 추가하면 마지막 은닉층에서 출력층으로 넘어갈때, 약 20%가 확률적으로 제외하게 됩니다. 수치로 계산하자면 64 * 0.2 = 7개가 누락되는 것입니다.
    layers.Dense(units=classes, activation='softmax'),
])

# model.compile(optimizer='adam',loss='mse')
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy', metrics=['accuracy'])
######## batch사이즈 정해보기
# history = model.fit(x,y, epochs=100)
# history = model.fit(x,y, epochs=100, batch_size=16, shuffle=True) # 셔플을 넣어주는 이유 3개분류가 되어있기 때문에 일부 데이터가 섞일수 있어 셔플 넣어줌
#Iris 데이터를 보면 0~2로 딱 3등분 이 되어있기 때문에 배치단위로 자르게 되면 특정 배치에만 0만 2만 3만 존재할 문제가 있기 때문에 셔플로 섞어주어야 한다.
# 더불어 이방식은 우선 메모리에 다 할당한 상태에서 배치사이즈를 나눈것이므로 메모리적으로는 이점이 없다는것을 인지해야합니다. 실제 데이터셋 설정 시에는 다른 방식을 사용해야 합니다.

##### early Stopping 과 checkpoint
save_path = "./model/iris_classification/ann_model.keras"
es = callbacks.EarlyStopping(monitor="val_loss", patience=10, verbose=1)
cp = callbacks.ModelCheckpoint(filepath=save_path, monitor="val_loss", save_best_only=True, verbose=1)

history = model.fit(x_, y_, epochs=120, batch_size=32, validation_split=.2, validation_batch_size=32, callbacks=[es,cp], shuffle=True)
##### 데이터 증강하기
# history = model.fit(x_,y_, epochs=100, batch_size=32, shuffle=True)

##### 바리데이션 데이터 배치사이즈
# history = model.fit(x_,y_, epochs=120, batch_size=32, validation_split=.2, validation_batch_size=32, shuffle=True)

history_ = history.history
# plt.plot(history['loss'])
##### 바리데이션 검증 데이터 평가 나옴
x_range = np.arange(1, len(history_['loss'])+1)
plt.plot(x_range, history_['loss'], x_range, history_['val_loss'])
plt.show()

plt.plot(x_range, history_['accuracy'], x_range, history_['val_accuracy'])
plt.show()

plt.plot(history['accuracy'])
plt.show()

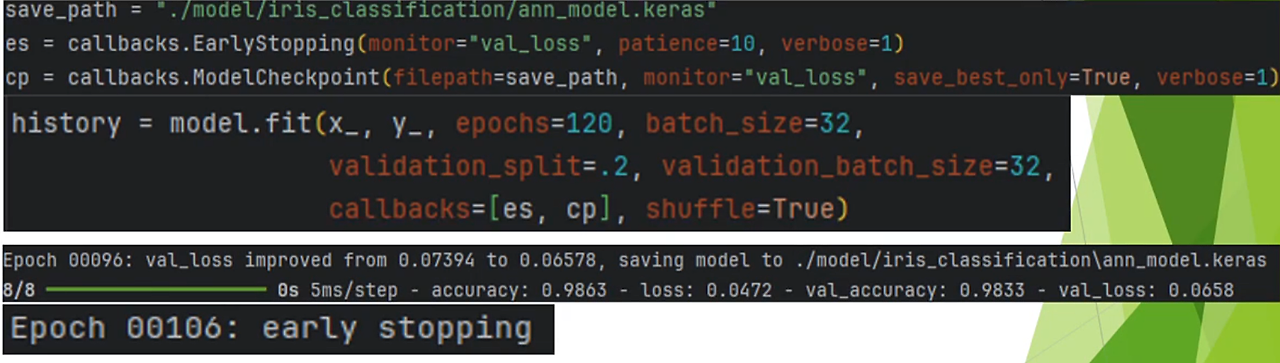
▶ 코드를 해석해보면 두 콜백 함수 모두에서 monitor는 작동하기 위해 바라보는 수치를 정하는 란입니다. 'val_loss'가 가장 좋은 편이며, Default값도 'val_loss'로 설정되어 있습니다.

▶ verbose는 콘솔에 출력되는 형식에 대한 정의입니다. 1번이 무난하게 보입니다.

▶ Early Stopping의 경우 patience인자가 있는데 이는 'val_loss'가 연속으로 k번 개선이 없다면 멈추라는 의미입니다. 학습이 개선되기까지 100번은 필요할 경우에는 'baseline'을 설정하여 patience가 적용되는 시점을 지정할 수 있습니다.

▶ Checkpoint의 경우 model을 저장할 공간에 대한 인자인 filepath와 저장방식에 대한 'save_best_only'가 있으며, 모델 전체가 아닌, 가중치만 저장하고 싶은 경우엔 'save_weight_only'인자를 사용하여도 됩니다.

▶ 파일명 저장시에 f-포맷팅의 방식으로 'epoch'나 'val_loss', 'loss' 등을 추가하여 파일명으로 출력하도록 할 수 있습니다.

728x90